(파동함수)
파형의 수학적 단순 표현: , where A is an amplitude
i) 정적 파형: ->
->
->
..... Eqn. (1)
ii) 동적 파형: 일정한 속도 로 이동하는 파동
시간 t 동안 이동한 거리 = , 따라서 Eqn. (1)에서 x 대신
대입
<- 각속도
, where
is frequency
..... Eqn. (2)
iii) 일반 파형 방정식: ..... Eqn. (3)
iv) 파형 방정식을 Eqn. (3)처럼 (왜 불필요 한 허수를 포함하여) 복소수로 나타낼까?
- 파동은 진폭과 파장, 진동수 그리고 위상으로 그 물리적 특성을 표현한다.
이때 이러한 물리적 특성을 가장 잘 그리고 편리하게 표현할 수 있는 방법이 필요
- 또한 파동들의 중첩, 간섭, 합성 등의 현상을 이해하기 위해서는 이러한 현상을 수학적으로
가장 편리하게 설명할 수 있는 방법이 필요
- 이러한 목적에 부합하는 수학적 도구가 바로 복소수 임. 이를 위해 다음을 살펴보자.
(복소수)
복소수의 정의: 실수 a와 b에 대해 로 표현되는 수, where
켤레(conjugate) 복소수:
복소평면:
직교 좌표계 복소평면 극 좌표계 복소평면
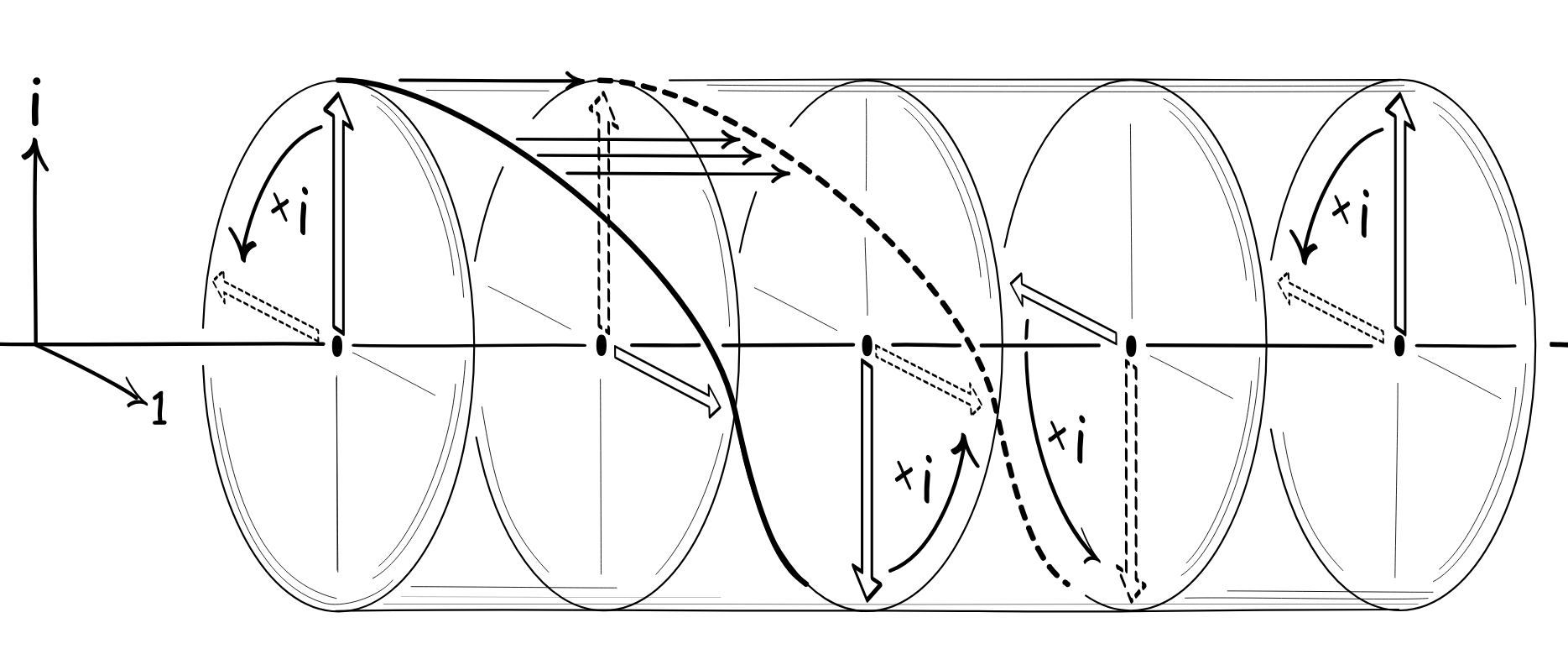
각속도 ω ( where T is period)로 복소벡터(z)가 회전한다고 할 때, 실수값과 허수값의 시간(t)에 따른 변화 (아래 그림)
Euler's Equation: (증명: 위키피디아)
(파동함수와 복소수)
Question ①: 파동은 진폭과 파장, 진동수 그리고 위상으로 그 물리적 특성을 표현한다.
Answer ①: 하나의 파동 함수를 복소평면 상에서 일정한 각속도로 회전운동하는 하나의 벡터로 표현할 수 있다. 이때, 벡터의 크기는 파동의 진폭(A)이 되고 각속도(ω)는 파동의 진동수(ν=ω/2π)가 되고 위상각(φ)은 파동의 위상(θ)으로 표현할 수 있다. 따라서 복소평면 상에서 회전운동하는 하나의 벡터로 하나의 파동이 가지는 제반 물리적 특성을 모두 표현(기술)할 수 있다.
Question ②: 파동들의 중첩, 간섭, 합성 등의 현상을 이해하기 위해서는 이러한 현상을 수학적으로 가장 편리하게 설명할 수 있는 방법이 필요
Answer ②: 삼각함수로 파동을 표현하면 이들의 중첩, 간섭, 합성의 결과에 따라 나타나는 파동함수 식을 계산하기가 수학적으로 상당히 복잡함. 반면 파동을 복소평면 상에서 회전운동하는 벡터로 표현하면, 서로 다른 진폭, 파장, 진동수, 위상을 가진 파동함수들의 중첩, 간섭, 합성의 결과를 계산하는 것이 마치 실수 벡터들 간의 연산처럼 편리하고 쉽게 계산될 수 있다.
Question ③ (출처: https://horizon.kias.re.kr/5848): 출렁거리는 파동을 기술한다라는 목적만을 생각한다면, 실수 함수인 사인이나 코사인 함수이면 충분할 것이다. 그런데 왜 굳이 허수를 변수로 갖는 지수 함수가 가장 순수한 형태의 파동을 기술한다고 주장하는 것일까?
Answer ③(출처: https://horizon.kias.re.kr/6063): 고전적인 파동의 대표격은 우리가 말을 하거나 음악을 들을 때 나오는 음파sound wave이다. 음파는 공기의 압력이 출렁거리는 파동이므로 실수 함수에 의해서 기술된다. 수학적으로 음파가 만족하는 미분 방정식은 다음과 같다.
위 고전적인 파동이 만족하는 미분 방정식은 시간에 대한 2차 편미분 값이 공간에 대한 2차 편미분 값에 비례한다는 것을 의미한다. 사인과 코사인 함수는 변수에 대한 2차 미분값이 자기 자신에 비례하므로 위 미분 방정식의 해가 될 수 있다. 재미있는 사실은 허수를 변수로 갖는 지수 함수도 위 미분 방정식의 해가 될 수 있다는 것이다. 하지만 그 이유는 약간 다르다. 지수 함수는 변수에 대한 1차 미분값이 자기 자신에 비례한다. 1차 미분값이 자기 자신에 비례하면 2차 미분값도 자기 자신에 비례하므로, 위 방정식의 해가 될 수 있다. 이런 미묘한 차이가 왜 중요할까?
시간에 대해서 1차 미분 방정식이면서 파동을 기술하는 가장 간단한 미분 방정식은 다음과 같다.
위에서 언급했듯이 파동 방정식이 시간에 대해서 2차 미분 방정식이었다면 사인이나 코사인 함수가 해가 될 수 있을 것이다. 하지만 여기서 주목할 사실은 파동 방정식이 시간에 대해서 1차 미분 방정식이기 때문에 그것의 해가 출렁거리는 파동을 기술하기 위해서는 허수가 필수적이라는 것이다!
슈뢰딩거 방정식이 시간에 대한 1차 미분 방정식이라는 성질이 (1)”파동 함수의 절대값의 제곱이 확률 분포이다”라는 조건과 (2)”확률 분포는 연속 방정식을 만족해야 한다”라는 조건을 동시에 만족시키기 위해서 절대적으로 필요했다는 사실이다. 양자역학에서 파동 함수의 확률론적 해석을 받아들이는 순간, 슈뢰딩거 방정식은 시간에 대한 1차 미분 방정식이어야 했고, 이 상황에서 파동을 기술하기 위해서는 허수가 반드시 필요했다. 양자역학은 태생적으로 허수의 존재를 절실히 요구했던 것이다!
댓글 0
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 16 | 재료신공정 실험실 특허발명 발명자 지분 계산표 | JooHwan | 2025.11.30 | 12 |
| 15 | 발명자의 요건 | JooHwan | 2025.11.23 | 11 |
| 14 | 광속 불변성과 E=mc2: Why light speed is constant And E=mc2 | JooHwan | 2025.08.08 | 149 |
| 13 | 파동의 양자화: Why Quantum Number Appears? | JooHwan | 2025.08.04 | 371 |
| 12 |
파동함수와 복소수: Why Wave Function is Complex Number
| JooHwan | 2025.08.02 | 128 |
| » |
파동함수와 복소수: Wave Function & Complex Number
| JooHwan | 2025.08.02 | 132 |
| 10 | 파동방정식: Derivation of Schrodinger Equation | JooHwan | 2025.07.27 | 1453 |
| 9 | 물질 상태와 불확정성 원리: State of Matters & Uncertainty Principle | JooHwan | 2025.07.26 | 233 |
| 8 | What Are Space and Existence? | JooHwan | 2025.07.06 | 143 |
| 7 | 공간(space) 그리고 존재(existence)란 무엇인가? | JooHwan | 2025.07.02 | 151 |
| 6 |
"How Big is Our World?“
| JooHwan | 2025.06.26 | 170 |
| 5 | "Is the World We Live In Three-Dimensional?" | JooHwan | 2025.06.26 | 181 |
| 4 |
이 세상의 크기는 얼마일까?
| JooHwan | 2025.06.26 | 304 |
| 3 | 우리가 살고 있는 세계는 3차원 일까? | JooHwan | 2025.06.24 | 175 |
| 2 |
청주한씨 시정공 종중 규약
| JooHwan | 2023.03.12 | 293 |
| 1 |
청주한씨 월포공 종중 대문계 규약
| JooHwan | 2023.03.12 | 260 |
